Boiling Water: Kettle vs Microwave

Introduction:

Now this is a rather unusual post, however I consider myself scientific and myself and a couple of colleagues (to those of you who know me reading this - I am of course talking about Tim and Alun) were debating the best way of heating water. Using a kettle, or a microwave.

There are many things to consider here covering the technical (power efficiency and theoretical capability) to practical (which one should you pick to make some tea). I'll try to cover both aspects here as best as I can measure.

There were various people ranting on the internet as you usually get, however it proved difficult to find actual data on the subject! So, I did it myself.

Hypothesis:

I am pro-kettle, I'm a firm believer that the kettle will consistently beat the microwave. There are however various pros and cons to both, technically and practically:

Pro-Kettle:

Technical:

• Uses more power, and will heat the water faster. While this seems irrelevant for electrical efficiency it means the water has less time to lose energy to it's surroundings.
• The kettle has a lid, which prevents (or limits) vapours escaping. Evaporation is a great way to lose energy (hence why we sweat when we're hot) so the kettle should have an efficiency gain here.
• Power is translated directly into heat. There is no intermediate as there is with a microwave (Power->Microwaves->Heat).

Practical:

• Uses significantly more power so boils water faster resulting in less time waiting about.
• Far more convenient for making multiple beverages simultaneously.
• Automated cut out when the correct temperature is reached - a microwave is prone to error.
• Latent heat in the element after heating and superior insulation means water stays hotter for longer and either does not require re-boiling (if you forget to make the tea) or takes less time / energy to re-boil.

Pro-Microwave:

Technical:

• Microwave radiation heats just the water molecules by causing them to vibrate, not the container.
• Water is heated all the way through and does not rely on convection currents to circulate the water from the bottom like a kettle.
• Once power is removed, there is no latent heat. A kettle retains heat in the element, thus wasting energy.

Practical:

• Only heats the amount of water you need. Kettles tend to be over-filled.
• A kettle collects limescale in the bottom and requires cleaning out periodically, no such problem with a microwave.
• A kettle is an additional appliance cluttering up the kitchen serving only a single function. A microwave is multi-purpose.

The Experiment:

Equipment:

• A kettle - Arendo 300821 (Rated 3kW)
  
• A microwave - Daewoo KOR-6N7RS (Rated 800W)
  
• A 1L plastic jug (I don't think it was microwave safe - didn't smell very good and got a bit floppy, but did the job).
  
• An electricity meter accurate to 1W - PowerLinkPlus ST010PM
  
• A timer - My trusty Casio F-91W digital watch
  

Method:

This experiment is simple enough. Use the kettle and microwave to heat up 1L of water straight from the tap. Record the amount of time it takes for the water to boil. This was repeated 4 times for the kettle and microwave.

Then an average of duration can be taken for both appliances, this average duration (in seconds) can then be multiplied by the actual power consumption (measured by the meter) to calculate the total amount of power (in Joules) required to heat the water.

Theory:

We have to assume a few things when running the calculations:

• Water comes out of the tap at 20 degrees C (I didn't have a thermometer).
• Water will be heated to 100 degrees C (Altitude and water impurities will change this).
• We use the average value of 4.19J to a calorie. The actual measurement varies depending on temperature.

We can calculate the theoretical amount of power required to heat this water. There is an 80 degree C difference between start and end temperature and it takes 1 calorie (about 4.19J) of energy to heat 1ml of water 1 degree C. So, to heat 1000ml by 80 degrees it'll take 80,000 calories which comes to 335,200J as our target minimum energy.

Results:

Observations and calculations:

The first thing I did was measure the actual power consumption of these devices. The microwave is rated at 800W. Of course, microwaves are not 100% efficient.

A quick google shows a magnetron has a rough efficiency of 65%. I measured the microwave at 1490W which gives it an efficiency of around 54% - but I've got no way of actually measuring the power of the microwave radiation so the 800W could be way off.

The kettle used 3055W so is considerably more powerful.

Raw Data:

Here's my results:

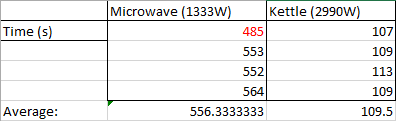
Now we can immediately see two things:

• I've got the microwave listed as 1333W in the above table but I said 1490W. Similarly the kettle is listed as 2990W however I said it was 3055W before.
• All of the results are fairly consistent except for the first result at 485 seconds which was considerably less than the last 3 (shown in red).

I have a theory which explains both points:

My initial measurement of energy consumption was when both appliances were cold and before they were used. I continued to monitor the energy consumption while the appliances were operating and the operating power decreased. I attribute this down to electrical resistance increasing as the temperature of the appliances increased with use. This increase in resistance leads to less current being drawn and given a constant voltage from the mains results in lower power output and thereby raising the time it takes to boil the water.

The microwave was more significantly impacted likely due to the inefficiencies of the magnetron combined with a fan inside cooling the magnetron down. This results in the warm up period taking longer and skews the respective data.

The average under the microwave column excludes the 485 second outlier.

Calculations and Conclusions:

Ideally we want to find how much energy it really took to perform these operations. From the data we have we can calculate this easily.

One Watt equals 1 Joule per second, we have the power usage of the appliance and the duration it was on, so it's simply a matter of multiplying the duration in seconds by the power in watts.

So, that gives us 741kJ for the microwave and 327kJ for the kettle to heat 1L of water.

This means that the kettle is about 56% MORE efficient than the microwave! I wasn't expecting a result anywhere near as conclusive.

However, there is a discrepancy, earlier I calculated that the theoretical minimum energy to raise water 80 degrees C is 335kJ so how have we got a result from the kettle that's just under that?!

Well, I made assumptions:

• That the water started at 20 degrees, the weather is pretty hot here so it might be a bit warmer than 20 to start with.
• That the water stopped at 100 degrees. I stopped the kettle and the microwave manually when the water appeared to be boiling, however in both cases it was not vigorously so some of the water may not have been at 100.
• I live in an area where there is a lot of limescale, and dissolved salts and impurities will lower the boiling point of water to below 100 degrees C.
• While fairly close, I do not live at sea level. This will also mean a lower air pressure and therefore a lower boiling point (but this will be very insignificant).

Even with these assumptions, the fact I got close to my calculated maximum efficiency I am happy with - and aligns with my original thoughts. The kettle is the most efficient way to heat your water! At least, from an electrical point of view.

Tying up loose ends:

Now, the numbers clearly support the kettle winning. However, it really does depend on the situation whether you use a microwave or kettle.

Arguably, a microwave will heat specifically one cup where a kettle is usually full (especially if the person using it isn't paying the darn electricity bill), so in that scenario it may be better to use a microwave.

It's also worth noting I have an exceptional kettle - the outside stays cool to the touch even after the kettle has finished boiling, and the water inside is too hot to touch after over an hour. (I found this out the hard way when emptying the kettle after this experiment).

One thing which was brought up in the conversation with my colleagues is that microwaves do not tend to get particularly hot - however, I can only attribute that to the length of time they're in operation. The 1L mark on the kettle is only about half way up the mark and is a fairly 'standard' amount of water to heat in a kettle. In a microwave you'd likely only be using a single cup. But after over 9 minutes of full power, the microwave was rather warm indeed - especially the casing area where the magnetron and transformer are located.

Big thanks to Tim and Alun for providing the surprisingly stimulating conversation about these appliances and inspiring me to spend my evening boiling water!